一个关于2016 IYPT No2 Lagging Pendulum的高中生解法
虽然不敢确定这不是正确的解法,但好歹是自己想出来,一个很简单的思路,用到了高中学的牛顿运动定律。
问题重述
Pendulum consists of a strong thread and a bob. When the pivot of the pendulum starts moving along a horizontal circumference, the bob starts tracing a circle which can have a smaller radius, under certain conditions. Investigate the motion and stable trajectories of the bob.
理想物理模型
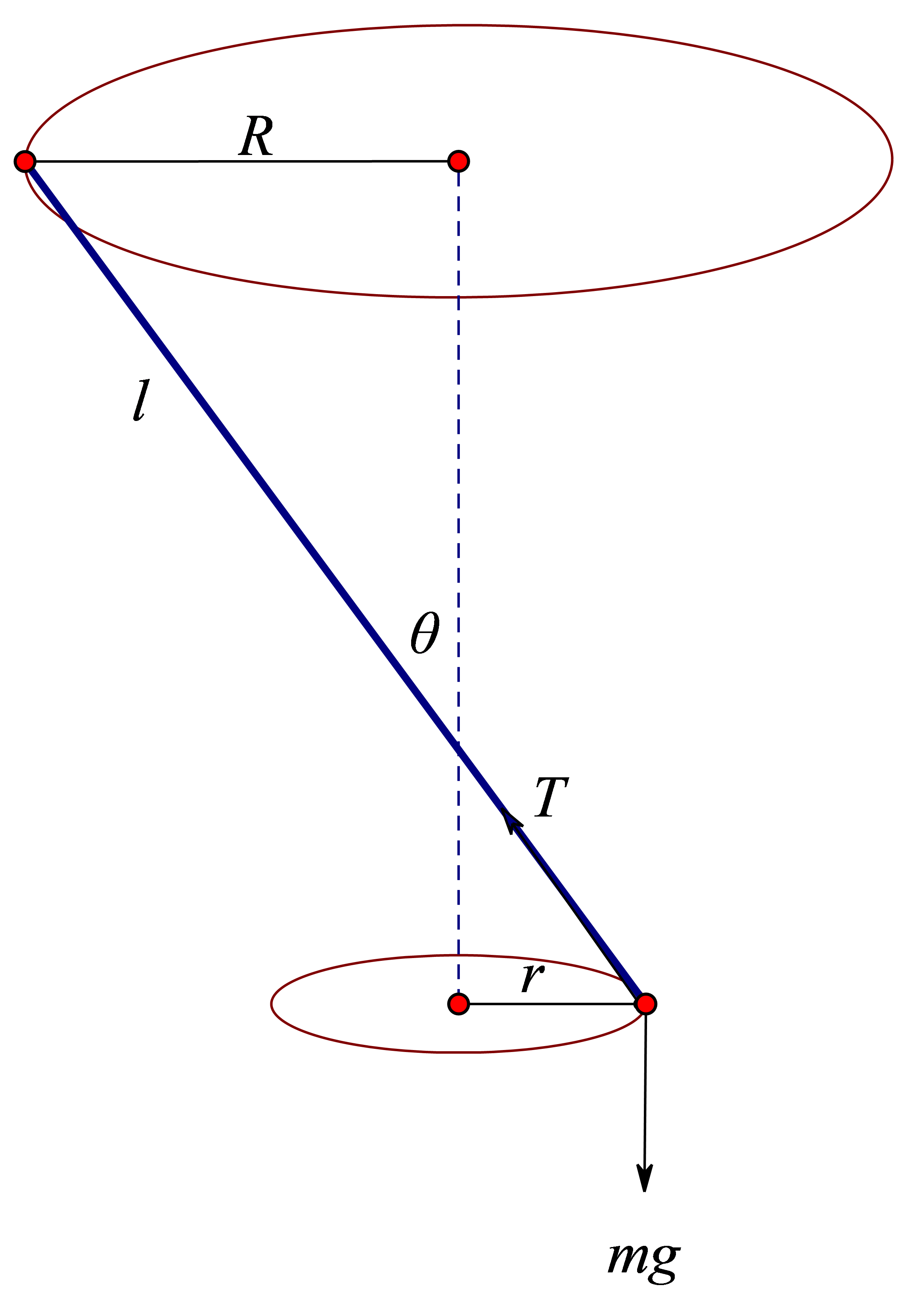
以重物为研究对象进行受力分析
$$T\sin \theta =\frac{m{{v}^{2}}}{r} $$
$$T\cos \theta =mg$$
$$v = \omega t $$
综合上式,得
$$\frac{g}{con\theta }=\frac{{{\omega }^{2}}r}{sin\theta }$$
而且,由二者的物理连接关系,有
$$\frac{R}{sin\theta}+\frac{r}{sin\theta}=l$$
所以模型的约束条件为
可计算得到重物的运动半径r及夹角$\theta $。此时,重物及悬挂点组成的系统的运动状态就可确定。
枢轴点(pivot)的运动方程
mathjax
\begin{align}
& x_0=R\cos (\omega t) \\
& y_0=R\sin (\omega t) \\
& z_0=8 \\
\end{align}
重物(bob)的运动方程
Matlab仿真
绘图程序
clear
clc
global R;R=10; %驱动点运动半径
global omega;omega=pi/3; %驱动点运动半径
global l;l=15;
global m;m=0.05;
global g;g=9.8;
t=linspace(0,100,1001);
j=0;
figure
title('The diagram of Lagging Pendulum');
axis([-20 20 -20 20 -7 10]);
grid on
hold on
plot3([0;0],[0;0],[10;-7],'k-.')
pause
for k=0:0.5:10
R=10+k;
j=j+11;
x0=[0.1;0.1];
options = optimoptions('fsolve','Display','iter');
[x,fval] = fsolve(@myfun,x0,options);
r=x(1)
theta=x(2)
th=theta./(2*pi).*180
x0=R.*sin(omega.*t);
y0=R.*cos(omega.*t);
z0=0.*t+8;
x1=r.*sin(omega.*t+pi);
y1=r.*cos(omega.*t+pi);
z1=z0-l*sin(theta)+0.*t;
h12=plot3([x0(1);x1(1)],[y0(1);y1(1)],[y0(1);y1(1)],'b-o','LineWidth',1.5);%画杆并取句柄
for i=j:j+10
set(h12,'XData',[x0(i);x1(i)],'YData',[y0(i);y1(i)],'Zdata',[z0(i);z1(i)]);
plot3([x0(i);x0(i+1)],[y0(i);y0(i+1)],[z0(i);z0(i+1)],'g')
plot3([x1(i);x1(i+1)],[y1(i);y1(i+1)],[z1(i);z1(i+1)],'r')
drawnow
end
end
非线性方程求解程序myfun.m
function F = myfun(x)
global R;
global omega;
global l;
global m;
global g;
F = [g/cos(x(2))-omega*omega*x(1)/sin(x(2));R/sin(x(2))+x(1)/sin(x(2))-l];
运行结果
基于这个模型,边界条件可以很粗暴将$R=r$代入上述约束条件,计算机跑一下可得想要临界速度$\omega$ 。